2021. 1. 23. 21:16ㆍ공부/Convex Optimization
Stanford 대학의 Convex Optimization 온라인 강의를 듣고 배운 개념을 정리한 글 입니다. 이 글은 강의에서 쓰는 교재를 참고하여 정리 하였습니다. 이 글을 읽기전 Introduction을 듣고 이 글을 읽는 것을 추천 드립니다.
Chapter 1 Convex sets
Chapeter 1에서는 Convex Optimization을 위한 Convex sets의 기본 개념을 다루고 있습니다. 최적화방법을 잘 알고 계신 분들은 Chapter 5부터 보시는 것을 추천드립니다.
1.1 Affine and convex sets
affine set과 convex set을 이해 하기위해서는 먼저 직선(line)과 선분(line segment)을 이해해야 한다.
- 직선(line) : 서로 다른 두점 \(x_1\)과 \(x_2\)를 지나는 선
- 선분(line segment) : 서로 다른 두점 \(x_1\)과 \(x_2\)를 이은 선
직선과 선분을 그림으로 나타내면 Figure 1.1과 같다.

1.1.1 Affine set
\(x_1 \ne x_2 \), \(x_1,x_2 \in C\)이고 \(C \subseteq R^n\)일 때, 두 점 \(x_1,x_2\)를 지나는 직선(line)이 집합 \(C\)에 포함되면 이 집합을 affine set 이라고 한다. 또, \(\theta \in R\)이면 점 \(x\)를 다음과 같이 \(x_1,x_2\)의 선형결합으로 나타낼 수 있다.
$$x= \theta x_1 + (1-\theta)x_2 ...(1)$$
위 (1)식에서 \(\theta\)의 값에 따라 \(x\)의 위치가 달라지게 된다. \(\theta\)의 범위를 나누면 다음과 같다.
- \(\theta < 0\)이면, 점 \(x \)는 \(x_2\)방향의 직선(line)위의 점이다.
- \(\theta > 1\)이면, 점 \(x \)는 \(x_1\)방향의 직선(line)위의 점이다.
- \(0 < \theta < 1\)이면, 점 \(x \)는 선분(line segment)위의 점이다.
- \(\theta = 0\)이면, \(x=x_2 \)이다.
- \(\theta = 1\)이면, \(x=x_1 \)이다.
\(\theta\)에 따른 점 \(x\)의 위치를 그림으로 나타내면 Figure 1.2와 같다.
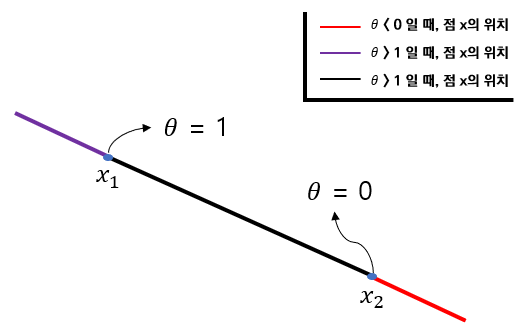
Figure 1.2 를 이해하기 위하여 (1)식을 다시 정리하면
$$ x = x_2 + \theta(x_1 - x_2)$$
와 같이 나타낸다. 즉, \(x\)는 점 \(x_2\)에서 \(x_1 - x_2\) 방향에 위치한 점이다.
affine set은 선형방정식의 해를 찾을때도 사용한다.
\(A \in R^{m \times n}\), \(b \in R^m\)이고 affine set \(C = \{x | Ax = b\}\) 일때, \(x_1,x_2 \in C\)라고 하면, \(Ax_1 = b\), \(Ax_2 = b\) 이다. 이때, \(Ax = b\)를 다음과 같이 나타낼 수 있다.
\(Ax=A(\theta x_1 + (1-\theta) x_2)\)
\(= \theta A x_1 + (1-\theta)A x_2\)
\(= \theta b + (1-\theta)b = b\)
즉, 모든 affine set은 선형방정식의 해집합(solution set)으로 나타낼 수 있다.
1.1.2 Convex set
Convex set은 affine set의 정의에서 직선(line)이 선분(line segment)로 바뀐 것이다. 다시 말하면 \(x_1 \ne x_2 \), \(x_1,x_2 \in C\)이고 \(C \subseteq R^n\)일 때, 두 점 \(x_1,x_2\)를 지나는 선분(line segment)이 집합 \(C\)에 포함되면 이 집합을 convex set 이라고 한다. 직선(line)이 아니고 선분(line segment)이기 때문에 (1) 식에서 \(0 \le \theta \le 1\)의 조건이 포함 되어야 한다.
convex set과 nonconvex set을 그림으로 표현 하면 Figure 1.3과 같다.

- ①은 서로 다른 두점이 집한 안 어디에 있든지 선분(line segment)이 집합안에 포함되므로 convex 하다.
- ②는 서로 다른 두점이 그림과 같이 존재하면 선분(line segment)이 집한안에 포함되지 않으므로 nonconvex 하다.
- ③은 거의 대부분 convex 하지만 서로 다른 두점이 그림과 같이 존재하면 선분(line segment)이 집합안에 포함되지 않으므로 nonconvex 하다.
1.1.3 Convex combination and convex hull
점 \(x_1,x_2,...,x_k\)를 이용하여 선형결합을 하면 다음과 같이 나타낼 수 있다.
$$x = \theta_1 x_1 + \theta_2 x_2 + ... + \theta_k x_k$$
이때, \(\sum_{k=1}^N \theta_i = 1\), \(\theta_i \ge 0\)을 만족하면 convex combination 이라고 한다.
다시말해, \(x_1,x_2,...,x_k \in C \)이고, 여기서 임의의 점들로 만든 convex combination이 집합 C에 속하면 집합 C는 convex set이라 할수 있다. 이때, 점들의 convex combination들이 집합 C에 속하면 집합 C를 convex hull 이라 하고 \(conv C\) 라고 표기한다. convex hull을 그림으로 표기하면 다음과 같다.

Figure 1.4와 같이 어떠한점들의 선형 결합이든지 집합 C에 포함되기 때문에 집합 C는 convex hull이다.
그레이엄 스캔 알고리즘(Graham's Scan Algorithm)을 이용하면 convex hull을 쉽게 찾을수 있다. Python을 활용한 그레이엄 스캔 알고리즘은 다음 포스팅에서 다뤄보도록 한다.
1.1.4 Convex cone
서로 다른 두점 \(x_1,x_2\)가 \(x_1,x_2 \in C\)이고 이 두점으로 만든 선형결합식이 다음과 같을때,
$$ x= \theta_1 x_1 + \theta_2 x_2 $$
\(\theta_1 \ge 0\), \(\theta_2 \ge 0\)과 같은 조건을 만족한다 하면, 위와 같은 식을 conic (nonnegative) combination 이라고 한다. 원점에서 시작된 직선이 서로 다른 두점 \(x_1,x_2\)를 지난다 했을때, conic combination은 다음과 Figure 1.5와 같이 한방향으로 무한히 진행되는 형태이다.
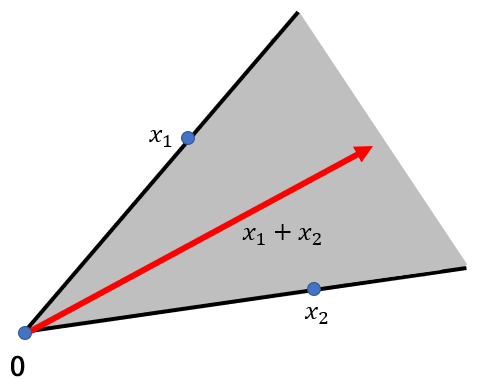
Figure 1.5에서 \(\theta_1 \ge 0\), \(\theta_2 \ge 0\)을 만족하는 모든 선형결합은 회색부분에 모두 속하게 된다. 이러한 conic combinatione으로 만들수 있는 모든 선형결합의 집합을 convex cone이라고 한다.
1.2 Some important examples of convex sets
1.2에서는 많이 기하학적으로 많이 알려진 평면에서의 convex set을 다룬다. 1.2를 다루기 전에 몇가지 수학기호와 용어에 대해서 알아야한다.
positive-define, positive semi-definite
\(n\ \times\ n\) 행렬 \(X\) 가 대칭행렬(symmetric matrix)일때 0이 아닌 모든 \(z \in R^n\)에 대하여 \(z^TXz\ > 0\)를 만족하면 행렬 \(X\)를 positive-definite라고 하고, \(X\)의 원소가 모두 양수이고, \(X \in S^n\) 이면 기호로 \(S_{++}^n\)라고 한다.
또, \(n\ \times\ n\) 행렬 \(X\) 가 대칭행렬(symmetric matrix)일때 모든 \(z \in R^n\)에 대하여 \(z^TXz\ \ge 0\)를 만족하면 행렬 \(X\)를 positive semi-definite라고 하고, \(X\)의 원소가 모두 0을 포함한 양수이고, \(X \in S^n\) 이면 기호로 \(S_{+}^n\)라고 한다. 대표적인 positive semi-definite에는 공분산 행렬(Covariance matrix)이 존재한다.

norm
norm은 벡터의 크기 또는 길이를 측정하는 방법이다. norm의 종류에는 보통 \(L_1\) norm, \(L_2\) norm, \(L_\infty\) norm 이 있다. 많이 쓰이는 \(L_1\),\(L_2\)를 보면 \(L_1\) norm은 \(\lVert\bullet\rVert_1\)로 나타내고 \(L_2\) norm은 \(\lVert\bullet\rVert_2\)로나타낸다.
\(L_1\) norm
\(L_1\) norm은 맨허튼 거리(Manhattan Distance)를 이용하여 벡터의 크기를 구하는 방법이다. 구하는 방법은 각 벡터의 모든 성분의 절대값을 더해주면 된다.
\(L_2\) norm
\(L_2\) norm은 유클리드 거리(Euclidean distance)를 이용하여 구하는 방법으로, 우리가 흔히 아는 좌표평면 위에서 두 점 사이의 거리를 구하는 공식이다.

1.2.1 Hyperplanes and halfspaces
$$ \{x | a^T x\ =\ b\} $$
\(a \in R^n\), \(\ a \ne 0\), \(b \in R\) 을 만족하면 Hyperplane(초평면)이라고 한다. 여기서 a와 x는 열벡터(coloum vector)이다. Hyerplane을 그림으로 표현하면 다음과 같다.

여기서 \((x-x_0)\)와 \(a\)는 직교한다. 따라서 다음 식을 만족한다.
$$ a^T(x-x_0)\ =\ 0 $$
$$ a^Tx-a^Tx_0\ =\ 0$$
$$ b\ = \ a^Tx_0 $$
따라서, \(b\ = \ a^Tx_0\)를 만족하고, b는 원점에서의 offset이기 때문에 affine set이자 convex set 이다. Hyperplane의 공식(\(a^Tx\ =\ b\))은 Optimization할 때 또는 지도학습 분류 모델인 SVM(Support Vector Machine)에서 자주 보이기 때문에 기억하도록 하자.
다음으로, Halfspace는 hyperplane경계를 포함한 한 쪽 공간을 말한다. Halfspace를 그림으로 표현하면 다음과 같다.

Halfspace는 Figure 1.7과 같이 hyperplane을 기준으로 두 부분으로 나눠지는데 보통 nomal vector a 의 방향에 따라 정해진다. Figure1.7과 같이 붉은색 구간에 vector a가 있으면 \(a^Tx \ge b\)로 표현하고, 회색구간 즉, -a 방향은 \(a^Tx \le b\)로 표현된다.

이제 halfspace의 성질을 확인 해보자. nomal vector a가 Figure 1.8과 같이 존재하면(halfspace가 회색부분 일때 : \(a^Tx \ge b\)), vector \((x_1-x_0)\)와 vector a는 예각(acute angle)이고 vector \((x_2-x_0)\)와 vector a는 둔각이다. 따라서, 항상 hyperplane의 nomal vecter a와 둔각을 이루는 vector 는 halfspace에 포함된다.
1.2.2 Euclidean balls and ellipsoids
Eclidean ball은 중심이 \(x_c\)이고 반지름이 r > 0인 원을 뜻한다. ball이 \(R^n\)에 존재할때, 다음 식과 같이 나타낸다.
$$ B(x_c,r)\ =\{x | \lVert x-x_c \rVert_2 \le r\}\ = \{x| (x-x_c)^T(x-x_c) \le r^2\} $$
위 식을 다시 나타내면 다음과 같이 된다.
$$ B(x_c,r)\ =\{x_c+ru | \lVert u \rVert_2 \le 1 \} $$
Euclidean ball이 convex set임을 증명하면 다음과 같다.
만약 Euclidean ball이 \(\lVert x_1-x_c \rVert_2 \le\ r\), \(\lVert x_2-x_c \rVert_2 \le\ r\)이고 \(0 \ge \theta \ge 1\)이면
$$ \rVert \theta x_1 + (1-\theta)x_2 -x_c \lVert_2\ =\rVert \theta(x_1-x_c)+(1-\theta)(x_2-x_c)\lVert_2 $$
$$ \le\ \theta \lVert x_1-x_c \rVert_2 +(1-\theta)\lVert x_2-x_c \rVert_2 $$
$$ \le\ r. $$
'공부 > Convex Optimization' 카테고리의 다른 글
| Chapter 2 Convex functions (0) | 2021.01.25 |
|---|